2.Temperature

-Temperature is an SI base quantity related to our sense of hot and cold. It is measured with a thermometer ,which contains a working substance with a measurable property , such as length or pressure, that changes in regular way as the substance becomes hotter or cooler.

-Temperature is an objective measurement of how hot or cold an object is. It can be measured with a thermometer or a calorimeter. It is a means of determining the internal energy contained within a given system.

-(In Physics term) Temperature (sometimes called thermodynamic temperature) is a measure of the average kinetic energy of the particles in a system. Adding heat to a system causes its temperature to rise.

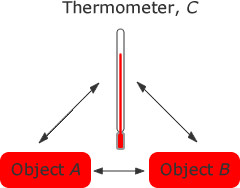
2.1 The zeroth law of Thermodynamics

The zeroth law of thermodynamics states that if two thermodynamic systems are each in thermal equilibrium with a third one, then they are in thermal equilibrium with each other.

In less formal language the message of zeroth law is :" Everybody has a property called temperature. When two bodies are in thermal equilibrium ,their temperatures are equal. And vice versa "We can now make our thermoscope or thermometer ,confident that its reading will have physical meaning. all we have to do is calibrate it.

Measuring Temperature

The Triple point of Water

Figure 18-4 shows a triple point cell , in which so-called triple point of water can be achieved in the laboratory.By international agreement, the triple point of water has been assigned by a value of 273.6K as the standard fixed point temperature for the calibration of thermometer that is T3=273.16k (triple point temperature) in which the subscript 3 means "triple point: this agreeement also sets size of the kelvin as 1/273.16 of the difference between the triple-point temperature of water and absolute zero

The constant Volume Gas Thermometer

The standard thermometer, against which all other thermometers are calibrated is based ont the pressure of a gas in a fixed volume .Figure 18-5 shows such a Constant-Volume gas thermomter;it consists  of gas-filled bulb connected by a tube to a mercury manometer. By raising and lowering reservoir R,the mercury level in the left arm of the U-tube can always be brought to the zero of the scale to keep the gas volume constant ( variation in the gas volume can affect temperature measurements).

We defined the temperature T as measured with a gas thermometer to be:

Here T is in kelvins and p3 and p are the pressures of the gas at 273.16K and the measured temperature respectively.

2.2 The celcius and farenheit Scales

Farenheit to celcius to kelvin comparison of standard temperatures

After we discussed kelvin scale, we now proceed to celcius and farenheit scales.Celcius scale ( formerly called Centigrade scale )is the sclae of choice for popular and commercial use and much scientific use. Converting kelvin scale to temperature scale :

where T is in kelvin unit 

And Tc is in degree celcius Unit 

The Fahrenheit scale,used in the United States,employs a smaller degree than the Celsius scale and a different zero of temperature.You can easily verify both these differences by examining an ordinary room thermometer on whichboth scales are marked.The relation between the Celsius and Fahrenheit scales is

 (equation 1)

where Tf is in Farenheit unit

By transposing the constant 9/5 and positive 32 to the other side of the equation we will get the temperature in degree celcius.

Temperature conversion formulas 

2.3 GAS LAWS

Ideal gas, or perfect gas, is the theoretical substance that helps establish the relationship of four gas variables, pressure (P), volume(V), the amount of gas(n)and temperature(T). It has characters described as follow:

1. The particles in the gas are extremely small, so the gas does not occupy any spaces.
2. The ideal gas has constant, random and straight-line motion.
3. No forces between the particles of the gas. Particles only collide elastically with each other and with the walls of container

3 GAS LAWS
A.) Boyles law- The absolute pressure exerted by a given mass of an ideal gas is inversely proportional to the volume  it occupies if the temperature and amount of gas remain unchanged within a closed system.Therefore the formula for boyles law is:

B.) Charles law- When the pressure on a sample of a dry gas is held constant the kelvin temperature and the volume will be in direct proportion.Therefore the equation for charles law is:

C.)Gay Lussac's Law
-It states that the pressure of a given mass of gas varies directly with the absolute temperature of gas, when the volume is kept constant.THerefore the equation for Gay Lussac's law is:

2.4 THERMAL EXPANSION

Thermal expansion is the tendency of matter to change its shape, area, and volume in response to a change in temperature.

Temperature is a monotonic function of the average molecular kinetic energy of a substance. When a substance is heated, the kinetic energy of its molecules increases. Thus, the molecules begin vibrating/moving more and usually maintain a greater average separation. Materials which contract with increasing temperature are unusual; this effect is limited in size, and only occurs within limited temperature ranges (see examples below). The relative expansion (also called strain) divided by the change in temperature is called the material's coefficient of thermal expansion and generally varies with temperature

Railroad

Railroad shows us the change in length because of the heat of the sun increasing more temperature received by the railroad.

The thermal expansion properties of some materials can be put to common use. Thermometers and thermostats may be based on the differences in expansion between the components of bimetalic strip.Also, the familiar liquid-in-glass thermometers are based on the fact liquids such as mercury and alcohol expand to a different (greater) extent that their glass containers.

Linear expansion

                                                    

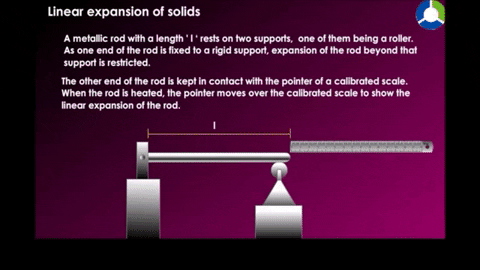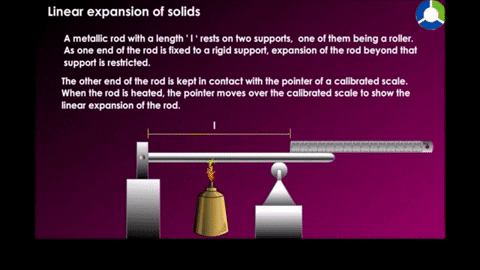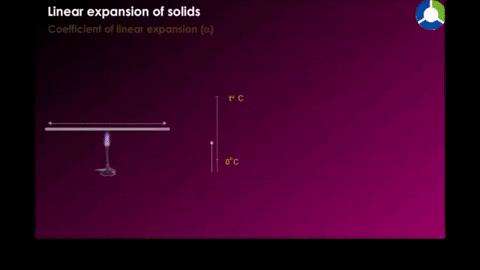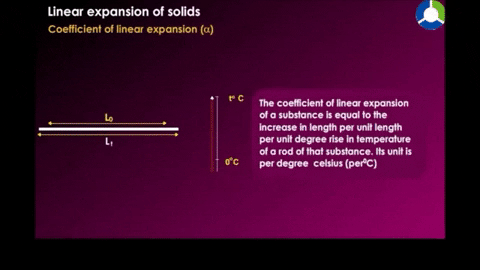
Figure 18-10

Some coefficients of linear expansion

Figure 18-10 Shows us that (a) A bimetallic strip, consisting of a strip of brass and a strip of steel welded together ,at temperature To. while (b) the strip bends as shown at temperatures above this reference temperature the strip bends the other way. many thermostats operate on this principle , making and breaking an electrical contact as the temperature rises and falls.




Example a temperature of a metal rod of length L is raised by an amount of change in temperature, its length is found to increase by an amount.


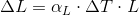
Where α is the constan called the coefficent of linear expression it has the unit "per degree" and depends on the material.See table 18-2 for some material's linear expansion.


Example of Linear Expansion:

An aluminum construction is designed for temperatures ranging -30^oC to 50^oC. If a beam's length is 6 m when assembled at 20^oC - the shortest final length of the beam at minimum temperature -30^oC can be calculated as 

L₁ = (6 m) + (6 m) (0.000023 m/m^oC) ((-30 ^oC) - (20 ^oC))

      =  5.993 m

The longest final length of the beam at maximum temperature 50^oC can be calculated as 

L₁ = (6 m) + (6 m) (0.000023 m/m^oC) ((50 ^oC) - (20 ^oC))

      =  6.004 m

Volume Expansion

 If we have linear Expansion .We also have Volume expansion same as Linear expansion if the temperature of solid object increased ,the volume of that solid object will increase also  .If the temperature of a solid or liquid whose volume is V is increased by an amount change in T, the increase in volume is found to be
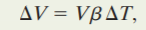                                                                                                                    where b is the coefficient of volume expansion of the solid or liquid. The coefficients of volume expansion and linear expansion for a solid are                                                    related by  :                     

Thermal Expansion of Liquids

The molecules of liquids are free to move in all directions within the liquid.On heating a liquid, the average amplitude of vibration of its molecules increases. The molecules push each other and need more space to occupy. The accounts for the expansion of the liquid when heated. The thermal expansion in liquids is greater than solids due to the weak forces between their molecules. Therefore, the coefficient of volume expansion of liquids is greater than solids.

Liquids have no definite shape of their own. A liquid always attains shape of their container in which it is poured.Therefore,when a liquid is heated, both liquid and the container undergo a change in their volume. Thus, there are two types of thermal volume expansion for liquid.

• Apparent volume expansion
• Real volume expansion

Table for volumetric thermal expansion coefficients of materials

Volume expansion example:

1.There are 500  cubic meter of air in a shop at 20.°C. What is the difference in volume if the temperature is 0°C? 

Formula for volume expansion:

Given volume of  air 500 cubic meter at 20.°C(initial temperature), and a 0°C(final temperature) subtituting this given value to the equation we get:

ΔV=(500)(3400x10^-6)(20-0)

ΔV=34 cubic meter

2.)At 30 degree celcius the volume of an aluminum sphere is 30 cubic cm.The coefficient of linear expansion is 24x10^-6 per degree celcius.If the final volume is 30.5 cubic cm,what is the final temperature of the aluminum sphere?

Given:

Initial Temperature =30 degree celcius

Initial volume=30 cubic cm

Final volume=30.5 cubic cm

change in volume =30.5-30=.5 cubic cm

find final temperature.

Solution:

=0.5cm^3=(72x10^-6/C)(30cm)(T2-30C)

T2=260C

Watch the video for better understanding in Temperature

Watch the video for better understanding in Thermal Linear expansion

Watch the video for better understanding in Thermal Volume expansion

Kindly answer this quiz to see how much you learn from this site

Quiz (Time limit:20 minutes, 10 items)

References:

1.) https://en.wikipedia.org/wiki/Thermal_expansion

2.)Fundamental of physics 10th editiion by jearl walker
3.)https://www.engineeringtoolbox.com/linear-thermal-expansion-d_1379.html

4.)https://www.scribd.com/document/374784329/Volume-Expansion-Problems-and-Solutions

5.)https://www.youtube.com/watch?v=ZoEY_51_fPY