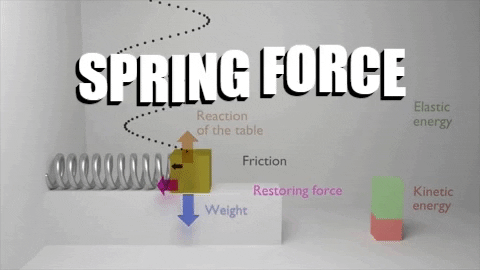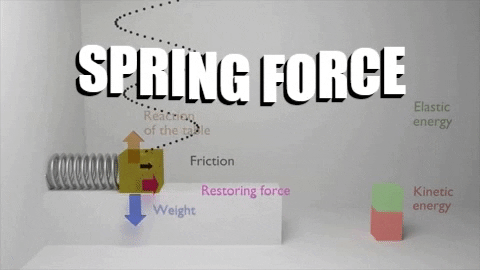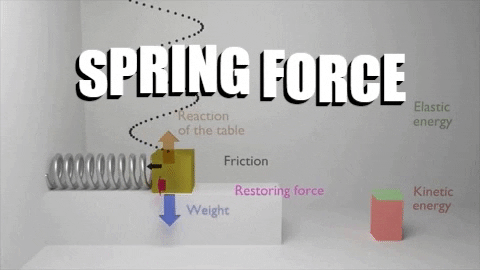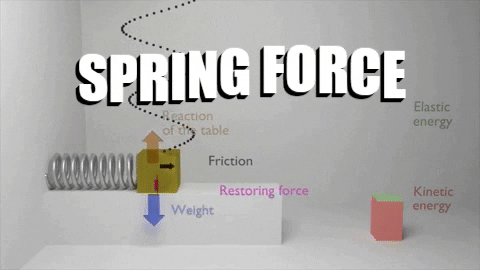
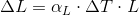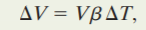Thermodynamics

Saturday, November 16, 2019

1. First law of Thermodynamics

Zeroth law of thermodynamics is the fundamentals of all laws it stated that the if two thermodynamics systems are each in thermal equilibrium with a third one, then they are in thermal equilibrium with each other this happens because they are transferring heat (in the form of energy) with each other until they reach their equal temperature the basic ideas why all these happens lies within the next law which is "the first law of thermodynamics".

The first law of thermodynamics stated that:

"The total energy of an isolated system is constant;energy can be transformed from one form to another, but can be created nor destroyed"

3 basic terms needed in thermodynamics
1.thermodynamics system - is everything inside the boundaries including the space
2. Sorroundings of a system-is everything of that system.The sum of the system and the sorroundings is the universe.
3.Boundary of a system- is the real or imaginary surface which separates that system from its sorroundings.

Types of System in thermodynamics
1.Closed System- type of system where only energy can cross the system boundaries
2.Open System - is a type of system where both mass and energy can cross the system boundaries
3.Isolated System-type of system where both mass and energy cannot cross the system boundaries.

(Image 1 )Bread inside the oven

Image 1 shows us an example of closed system where the system is whats inside the oven(bread) including the space. When heat is transfer or added into the system there is the change in internal energy due to rise in temperature,an increase in temperature or a change in state.

Internal energy is the energy contained within the system, excluding the kinetic energy of motion of the system as a whole and the potential energy of the system as a whole due to external force fields.

Formula for internal energy:
ΔU =Q – W

where Q is the heat flowing in or out the system ,W is the work done by or onto the system and U is the internal energy.

Sign convention

When heat is supplied to the system, it increases the internal energe, so Q is taken as positive(Q > 0)
Work was done on the system also increases the internal energy, so it is also taken as positive. (W > 0),In this case, the first law of thermodynamics is written as:

ΔEint=Q +W

When heat is rejected by the system,it decreases the internal energy, so it is taken as negative. (Q <0)
Work done by the system decreases the internal energy, so it is taken as negative (W <0)

Example of first law of thermodynamics
One example of first law of thermodynamics is the diesiel engine When an engine burns fuel it converts the energy stored in the fuel's chemical bonds into useful mechanical work and into heat.

The conservation of energy principle defined by the first law of thermodynamics says that when all of the fuel's energy is released by burning in the engine's cylinders it doesn't disappear. The total quantity of energy stays the same and must be accounted for. In the case of the diesel engine shown below it either becomes thermal energy (heat) or mechanical energy (work). For every 100 units of fuel energy that is burned in the engine a hundred units of converted energy has to end up somewhere. It doesn't disappear

Application of First law of Thermodynamics
1.)Adiabatic process - it is a process which no heat can transfer in or out the system. There is no transfer in heat so Q=0

ΔEint=Q +W

since

Q = 0 ,SO

ΔEint = W

2.) Isovolumetric Process-A process where volume is held constant, since volume remains constant, the work done will be zero W=0.

ΔEint =Q +W

Since W=0,SO

⇒ Q = ΔEint

3.)Isothermal process-A process in which temperature held constant, Since the temperature remains constant in this process so the internal energy also must remain constant :

ΔEint=Q +W

0 = Q + W

⇒ Q =-W

4.) Isobaric process- A process in which pressure held constant.

$Q=\Delta U-W\,$

where:

$W=-n\,R\,\Delta T$

and

{\begin{aligned}Q&=n\,c_{V}\,\Delta T+n\,R\,\Delta T\\&=n\,\left(c_{V}+R\right)\,\Delta T\\&=n\,c_{P}\,\Delta T\end{aligned}}

Problem examples:

1.Assume that there is no change in internal energy while the system is doing work of 20J .Compute for the heat added or taken away by the system.

Our formula for internal energy is

ΔEint=Q -W(Negative because the system is the one doing work)

given that there is no change in internal energy (ΔEint =0) while the system is doing work of 20J (W=20J).Subtituting it to our formula we get:

0=Q-20

Q=20J

The heat added to our system is 20J when the system did 20J of work.

2.A bottled water with the heat of 5J is placed on a tracking field exposed by a sun giving more 20J of heat ,Compute for the work done by or onto the bottled water if the bottled water has the change in internal energy of 40J.

Our formula for Work is

W = ΔEint - Q

given 20J plus 5J of heat and 40J of change in internal energy we get:

W = 40J-(20+5)

W=15J

The work in the system is 15J.

3. A balloon having a gas initial volume of 3L .The balloon transfers 300J of heat to the sorroundings this makes the gas final volume 1.7L. Compute for the internal energy given our external pressure 1x10⁵

Formula for internal energy given pressure and volume is :

ΔEint=−PΔV+ Q

Given pressure 100000 Pa ,Transfer of heat 300J and change in volume from 3L to 1.7L Subtituting these to the equation we get:

ΔEint= -(100000Pa)(3L-1.7L) - 300J = -130300J

Watch video for broad and clear explanation of First law of thermodynamics and internal energy:

watch the video of me Explaining the summary of First law of thermodynamics

Kindly answer this quiz to see how much you learn from this site:

Quiz (time limit :20 minutes , 10 items)

References:

1.https://www.youtube.com/watch?v=Xb05CaG7TsQ

2.https://physicsabout.com/first-law-of-thermodynamics/

3.http://www.ftexploring.com/energy/first-law_p2.html

4.https://www.youtube.com/watch?v=4i1MUWJoI0U&t=17s

Sunday, November 3, 2019

2.Temperature

-Temperature is an SI base quantity related to our sense of hot and cold. It is measured with a thermometer ,which contains a working substance with a measurable property , such as length or pressure, that changes in regular way as the substance becomes hotter or cooler.

-Temperature is an objective measurement of how hot or cold an object is. It can be measured with a thermometer or a calorimeter. It is a means of determining the internal energy contained within a given system.

-(In Physics term) Temperature (sometimes called thermodynamic temperature) is a measure of the average kinetic energy of the particles in a system. Adding heat to a system causes its temperature to rise.

2.1 The zeroth law of Thermodynamics

The zeroth law of thermodynamics states that if two thermodynamic systems are each in thermal equilibrium with a third one, then they are in thermal equilibrium with each other.

Image result for zeroth law of thermodynamics

In less formal language the message of zeroth law is :" Everybody has a property called temperature. When two bodies are in thermal equilibrium ,their temperatures are equal. And vice versa "We can now make our thermoscope or thermometer ,confident that its reading will have physical meaning. all we have to do is calibrate it.

Measuring Temperature

The Triple point of Water

Figure 18-4 shows a triple point cell , in which so-called triple point of water can be achieved in the laboratory.By international agreement, the triple point of water has been assigned by a value of 273.6K as the standard fixed point temperature for the calibration of thermometer that is T3=273.16k (triple point temperature) in which the subscript 3 means "triple point: this agreeement also sets size of the kelvin as 1/273.16 of the difference between the triple-point temperature of water and absolute zero

The constant Volume Gas Thermometer

The standard thermometer, against which all other thermometers are calibrated is based ont the pressure of a gas in a fixed volume .Figure 18-5 shows such a Constant-Volume gas thermomter;it consists of gas-filled bulb connected by a tube to a mercury manometer. By raising and lowering reservoir R,the mercury level in the left arm of the U-tube can always be brought to the zero of the scale to keep the gas volume constant ( variation in the gas volume can affect temperature measurements).

We defined the temperature T as measured with a gas thermometer to be:

Here T is in kelvins and p3 and p are the pressures of the gas at 273.16K and the measured temperature respectively.

2.2 The celcius and farenheit Scales

Farenheit to celcius to kelvin comparison of standard temperatures

Image result for kelvin celsius fahrenheit

After we discussed kelvin scale, we now proceed to celcius and farenheit scales.Celcius scale ( formerly called Centigrade scale )is the sclae of choice for popular and commercial use and much scientific use. Converting kelvin scale to temperature scale :

where T is in kelvin unit

And Tc is in degree celcius Unit

The Fahrenheit scale,used in the United States,employs a smaller degree than the Celsius scale and a different zero of temperature.You can easily verify both these differences by examining an ordinary room thermometer on whichboth scales are marked.The relation between the Celsius and Fahrenheit scales is

(equation 1)

where Tf is in Farenheit unit

By transposing the constant 9/5 and positive 32 to the other side of the equation we will get the temperature in degree celcius.

Temperature conversion formulas

2.3 GAS LAWS

Ideal gas, or perfect gas, is the theoretical substance that helps establish the relationship of four gas variables, p ressure (P), volume(V), the amount of gas(n)and temperature(T). It has characters described as follow:

The particles in the gas are extremely small, so the gas does not occupy any spaces.
The ideal gas has constant, random and straight-line motion.
No forces between the particles of the gas. Particles only collide elastically with each other and with the walls of container

3 GAS LAWS
A.) Boyles law- The absolute pressure exerted by a given mass of an ideal gas is inversely proportional to the volume it occupies if the temperature and amount of gas remain unchanged within a closed system.Therefore the formula for boyles law is:

B.) Charles law- When the pressure on a sample of a dry gas is held constant the kelvin temperature and the volume will be in direct proportion.Therefore the equation for charles law is:

C.)Gay Lussac's Law
-It states that the pressure of a given mass of gas varies directly with the absolute temperature of gas, when the volume is kept constant.THerefore the equation for Gay Lussac's law is:

2.4 THERMAL EXPANSION

Thermal expansion is the tendency of matter to change its shape, area, and volume in response to a change in temperature.

Temperature is a monotonic function of the average molecular kinetic energy of a substance. When a substance is heated, the kinetic energy of its molecules increases. Thus, the molecules begin vibrating/moving more and usually maintain a greater average separation. Materials which contract with increasing temperature are unusual; this effect is limited in size, and only occurs within limited temperature ranges (see examples below). The relative expansion (also called strain) divided by the change in temperature is called the material's coefficient of thermal expansion and generally varies with temperature

Railroad

Railroad shows us the change in length because of the heat of the sun increasing more temperature received by the railroad.

The thermal expansion properties of some materials can be put to common use. Thermometers and thermostats may be based on the differences in expansion between the components of bimetalic strip.Also, the familiar liquid-in-glass thermometers are based on the fact liquids such as mercury and alcohol expand to a different (greater) extent that their glass containers.

Linear expansion

Animated GIF

Figure 18-10

Some coefficients of linear expansion

Figure 18-10 Shows us that (a) A bimetallic strip, consisting of a strip of brass and a strip of steel welded together ,at temperature To. while (b) the strip bends as shown at temperatures above this reference temperature the strip bends the other way. many thermostats operate on this principle , making and breaking an electrical contact as the temperature rises and falls.

Example a temperature of a metal rod of length L is raised by an amount of change in temperature, its length is found to increase by an amount.

Linear thermal expansion formula: Change in length = coefficient of linear thermal expansion x change in temperature x initial length

Where α is the constan called the coefficent of linear expression it has the unit "per degree" and depends on the material.See table 18-2 for some material's linear expansion.

Example of Linear Expansion:

An aluminum construction is designed for temperatures ranging -30^oC to 50^oC. If a beam's length is 6 m when assembled at 20^oC - the shortest final length of the beam at minimum temperature -30^oC can be calculated as

L₁ = (6 m) + (6 m) (0.000023 m/m^oC) ((-30 ^oC) - (20 ^oC))

= 5.993 m

The longest final length of the beam at maximum temperature 50^oC can be calculated as

L₁ = (6 m) + (6 m) (0.000023 m/m^oC) ((50 ^oC) - (20 ^oC))

= 6.004 m

Volume Expansion

If we have linear Expansion .We also have Volume expansion same as Linear expansion if the temperature of solid object increased ,the volume of that solid object will increase also .If the temperature of a solid or liquid whose volume is V is increased by an amount change in T, the increase in volume is found to be

where b is the coefficient of volume expansion of the solid or liquid. The coefficients of volume expansion and linear expansion for a solid are related by :

Thermal Expansion of Liquids

The molecules of liquids are free to move in all directions within the liquid.On heating a liquid, the average amplitude of vibration of its molecules increases. The molecules push each other and need more space to occupy. The accounts for the expansion of the liquid when heated. The thermal expansion in liquids is greater than solids due to the weak forces between their molecules. Therefore, the coefficient of volume expansion of liquids is greater than solids.

Liquids have no definite shape of their own. A liquid always attains shape of their container in which it is poured.Therefore,when a liquid is heated, both liquid and the container undergo a change in their volume. Thus, there are two types of thermal volume expansion for liquid.

Apparent volume expansion
Real volume expansion

Table for volumetric thermal expansion coefficients of materials

Volume expansion example:

1.There are 500 cubic meter of air in a shop at 20.°C. What is the difference in volume if the temperature is 0°C?

Formula for volume expansion:

Given volume of air 500 cubic meter at 20.°C(initial temperature), and a 0°C(final temperature) subtituting this given value to the equation we get:

ΔV=(500)(3400x10^-6)(20-0)

ΔV=34 cubic meter

2.)At 30 degree celcius the volume of an aluminum sphere is 30 cubic cm.The coefficient of linear expansion is 24x10^-6 per degree celcius.If the final volume is 30.5 cubic cm,what is the final temperature of the aluminum sphere?

Given:

Initial Temperature =30 degree celcius

Initial volume=30 cubic cm

Final volume=30.5 cubic cm

change in volume =30.5-30=.5 cubic cm

find final temperature.

Solution:

=0.5cm^3=(72x10^-6/C)(30cm)(T2-30C)

T2=260C

Watch the video for better understanding in Temperature

Watch the video for better understanding in Thermal Linear expansion

Watch the video for better understanding in Thermal Volume expansion

Kindly answer this quiz to see how much you learn from this site

Quiz (Time limit:20 minutes, 10 items)

References:

1.) https://en.wikipedia.org/wiki/Thermal_expansion

2.)Fundamental of physics 10th editiion by jearl walker
3.)https://www.engineeringtoolbox.com/linear-thermal-expansion-d_1379.html

4.)https://www.scribd.com/document/374784329/Volume-Expansion-Problems-and-Solutions

5.)https://www.youtube.com/watch?v=ZoEY_51_fPY

1.Work and kinetic Energy

This video explains the definition of work and enery.(Youtube channel:Professor Dave explains)

Image result for picture of work force x distance

Work is an action that is performed on an object or system and that transfers energy from one location to another or from one form to another. The basic mathematical formula is :

work = force x distance or W = FD

kinetic energy (K) is the energy while the object or matter is in state of motion. If the object moves faster the greater the kinetic energy it posses.When the object is stationary or not moving the kinetic energy is zero. Now we all know that Work is equal to the energy we possess so we can say that W=FD=KI =(1/2)(mv２). Unit of Work and energy are the same .

Mathematical explanation why work is equal to the kinetic energy .

We all know that the common formula of force is :
F=ma (equation 1 )
where m is the mass of an object and a is the acceleration of an object . As the object moves through a displacement ,the force changes from an initial value Vo(Initial velocity) to some other value Vf(Final velocity) . But when the force is constant , We all know that the acceleration is also constant so using the formula of constant acceleration which is :

equation 2

using equation 1 we get a=f/m ,subtituting a to equation 2 we get:

Multiplying both sides by distance and dividing both sides by 2 we get:

equation 3

The first term is the Final kinetic energy or the kinetic energy at the end of displacement while the second term is the kinetic energy at the start these tells us that the kinetic energy has been changed by the force . while on the right side of equation 2 tells us that the change in kinetic energy is equal to the Force multiply to distance(FD).
take note: to calculate the force does on an object through some displacement we must use the force component along the objects displacement. the force perpendicular to the displacement does zero work.

Kinetic energy and work Theorem

As we observe on our equation 3 we can tell that left side equation is the change in kinetic energy and right side equation is the work .For the particle-like object we can generazlize: Let △K be the change in kinetic energy of the object and let W be the net work done on it . Then

(equation 4)

which says that:

(Change in the kinetic energy of a particle)=(net work done on a particle)

we can also write:

which says that kinetic energy after the net work is done is equal to kinetic energy before the net work plus the net work done. Since there is no speed or velocity in initial kinetic energy V=0 we can say that:

(Equation 5)

Example 1:

A factory worker pushes a Crate from building A to building B with a distance of 400m and a constant velocity of 1 meter per second he pushes the crate with a force of 50 N .A.) Compute for the work done in moving the crate B.) Compute the mass of the crate .

Solution :

A.)

We all know that the formula of work is the force applied to the object multiply to the distance from starting point to some point .We say that:

B.)

Computing for the mass We need equation 5

Where K= (1/2)mV^2 equating to mass we get:

1.1 Work done by Gravitational Force

Gravity is defined as the force that attracts a body towards the earth or towards any other physical body having mass.

If a particular object is falling, the particle is bound to point in the direction of gravity. The magnitude of the falling body depends on the mass, gravitational constant and height from which it is falling.

Figure 1

The formula for work done by a gravity is:

(equation 6)

When the Particle like object is rising , the Gravity force is directed opposite to the displacement as indicated in figure 1.

when the particle like object reach the maximum height and falls down the angle between the displacement and the gravitational force becomes 0 because they are acting on same direction which is downward. this will give us :

Our equation becomes positive because gravitational force transfer energy to the kinetic energy of falling object Thus the speed of the object is now increasing .

Example :

A ball with a mass of 600g is being shot from a free throw line and luckily shoots in the ring . Compute for the work done by the gravitational force on the ball starting from when it hits the ring until it drops on the floor .The height of the ring is 10ft from the ground.

Work done in lowering and lifting an Object

Now imagine you are lifting a table by applying a vertical force (F) to it.

During the upward displacement ,the vertical force applied to the table does positive work while the gravitational force does negative work .The applied force transfer energy to it while the gravitational force transfer energy from it thats why it is easier to lowered the table than to lift it because the gravitational force is always pointing towards the center of the earth.By using equation 4 ,the change in kinetic energy of the table due to the energy transfer from gravitational force and due to the energy applied to the force is :

(equation 7)

(equation of change in kinetic energy due to applied force and gravitaional force)

This equation can also apply on lowering an object but the gravitational force is now transferring the energy to the table while the applied force is now transferring energy from it.

If an object is stationary before and after a like picking up a bottle of water from the floor and put it inside the refrigerator this will give us zero in final kinetic energy and initial kinetic energy.We can rewrite equation 6 as:

(equation 8)

take note that we get the same equation if Kf and Ki is not zero but same in value .Eitherway equation 8 tells us that the work done by the applied force is equal to the negative work done by the gravitational force .Using equation 6 we can rewrite equation 8 as :

(Work done in lifting and lowering the object;Kf=Ki)

Example:

A wall clocked having a mass of 400g is dropped on the floor and picked up to put it back on the wall with a height of 8ft compute for the applied force needed to put back the wall clock.

Solution:

Our formula for work is :

Work = Mass * Gravity * Height

Given Constant gravity force=9.8 m/s^{2 ,}mass=400g,height of 8Ft .

W=(400g)(9.8)(8Ft.)

W=31360J

1.2 Work done by a Spring Force

Figure 2

Figure 2 shows a blocked attached to the spring with the pring parrallel to the X axis and the relaxed state of the blocked attached to the spring is at the origin of x axis .

Figure 2(a) shows that the spring is on a relaxed state this means there is no force acting and there is no displacement yet .On figure 2(b) it shows that the blocked attached to the spring is being pulled so our displacement is pointing toward the positive side of X - axis .Figure 2(c) shows that the block attached to the spring is being pushed so the displacement of the block is going to the negative side of X-axis.

The formula for Force exerted by the spring is :

Where k is called the Spring constant or Constant force this is the measure of the stiffness of your Spring ."x" is the displacement of the block in the X-axis.

If and object is attached to the spring's free end , the work Ws done on the onject by the spring force when the object moved from an initial position to final position is

If Xi=0 and Xf=X, then the equation becomes

Example 1: If the force stretch a spring given by (80N/m)(x) ,compute for the work needed to stretch the spring 7m from rest?

1.3 Work done by a Variable Force

If the force varies (e.g. compressing a spring) we need to use calculus to find the work done.

If the force is given by F(x) (a function of x) then the work done by the force along the x-axis from a to b is:

$\displaystyle{W}={\int_{{a}}^{{b}}}{F}{\left({x}\right)}{\left.{d}{x}\right.}$

The meaning of Variable Force is when an object needs or requires increasing force for it to moves from one point to another.Like the car shown below The car moves faster and faster because of the driver increasing engine force to increase the speed of the wheel.
If you observed the formula of Work define by variable force the integration from a to b with respect to function x is equal to the force varying in the displacement X or in a floor surface .